
As I told you last week, we've had a very satisfying reaction to the puzzles we've featured here. Perhaps a word of explanation would be proper at this point.
Everyone in the world, to some extent, is in show business, whether they recognize it or not. There's a very strong element in anyone's lifestyle - designed by trial-and-error - that enables us to "put on an act" as a survival technique. You can see the ghost of Natural Selection in the background here, so I won't spend much time on that aspect. But this show business facet of my personality urges me to use the experience I've acquired over the past seven decades, as a teaching tool.
Part of the regular work here at the JREF is sending out representatives to classrooms and auditoriums, both locally and internationally, to deliver lectures that entertain while they educate. This Web page, too, reaches a lot of people, and the "showbiz" gimmick of offering puzzles not only got your attention, but also illustrated the process of thinking - critical thinking - which I'm very happy to tell you was demonstrated rather spectacularly through your answers, solutions, and comments. Andrew Harter and I have been reading them every day, and continue to do so, with great delight.
I'm asking you, as a fan of the JREF, to work on instilling the curiosity and ingenuity that you have shown, into the young people that you meet. Show them that solving problems can be fun as well as productive. Now, it's true that these specific puzzles will probably not lead you or those young people to practical solutions in everyday life, but it's the process of critical thinking - and the delight that can be experienced in that process - that is important here.
Enough philosophy! Before I go any further, I must announce that only three persons correctly solved the Man-in-a-Wheel problem, and saw through the "trick question" aspect. However, we're still welcoming responses to that one, which will be explained next week.. This week, we have enough of a job just giving you the "19 Cogged Wheels" solution. So here goes:

Though we had a great number of correct answers for the easiest scenario, particularly after we revealed that the magic word was "Möbius," many folks failed to recognize that name, much to my surprise. August Ferdinand Möbius (1790-1868) was a German mathematician who is best remembered, perhaps, and unfairly, for his small invention known as the Möbius Strip, or Möbius Band. The idea is illustrated here. You can make a model of this interesting item simply by cutting a long strip of newsprint (oh, go ahead and use adding-machine paper if you wish!) and gluing the ends together so that it makes a loop - but first, giving one end of the strip a half-twist.
Starting at any place on the loop, draw a line along the center of the strip, continuing until you come back to your starting place. Lo! You have now covered BOTH SIDES of the loop, without passing over an edge. So, this strange item has only one side....! If you were to paint it, as we've done in the illustration, your brush would never have to leave the surface, yet the entire strip would be painted.
What has this got to do with 19 gears, you ask. Well, the number one solution to the problem is to give the odd number of cogged wheels a half-twist, thus reversing the parity of the system and allowing all of the gears to turn. Hold on! What's this "parity" business? Well, it's a mathematical term that means "equivalence," or "similarity." To best illustrate it, imagine that you have the simple task of simply turning over a coin a given number of times. If that number is an odd number, you will always end up with the "other side" of the coin facing you. If the number is even, you'll end up with the "same side" of the coin facing you. With the cogged-wheel problem, a set of wheels that is even will always turn; a set that is odd will never turn - except if you have applied one of our three solutions to the problem.
(No, I will not enter into discussions of whether you reverse parity in the coin-turning task by standing on your head!)
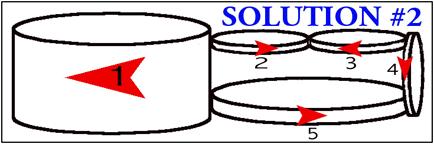

That's one solution, by far the easiest and the one most often given by our readers. Now here's a much more interesting one, with two variations. I think the illustrations explain it all. These were submitted as two different solutions, but they're essentially the same, topologically. In both cases, one wheel merely serves to reverse the parity - wheel #1 in illustration 2, the bottom wheel in 2a. Please excuse illustration 2a. It's taken right from my scratch pad, since I had no time this week to work on it.
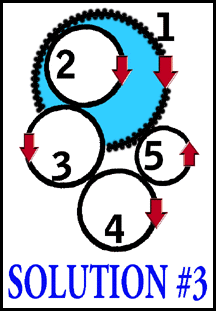 And finally, the third solution. This calls for a
variation of the regular cogged wheel, using one wheel that has
the cogs on the inside. The others are cogged on their outside
edges. In the illustration, wheel No. 1 - the blue one - is that
special wheel. Again, this is where the parity is switched. Wheel
No. 2 is "taller" than the others so that it is driven
by wheel No. 1 and in turn it extends up and drives No. 3. Wheel
No. 5 is also "taller" - or "deeper," if
you wish, so that it will engage wheel No. 1.
And finally, the third solution. This calls for a
variation of the regular cogged wheel, using one wheel that has
the cogs on the inside. The others are cogged on their outside
edges. In the illustration, wheel No. 1 - the blue one - is that
special wheel. Again, this is where the parity is switched. Wheel
No. 2 is "taller" than the others so that it is driven
by wheel No. 1 and in turn it extends up and drives No. 3. Wheel
No. 5 is also "taller" - or "deeper," if
you wish, so that it will engage wheel No. 1.
There are a few other solutions, none of which I accepted because they are such very special cases. For example, any set of "crown" gears brought together (an even number that is!) in a similar configuration will work, and the three solutions given above will also apply.
To forestall an avalanche of email messages, I will add here that in Solution No. 1, above, the chain of gears can be twisted more than half a turn. The number of turns needed to change the parity is: (2n-1)/2, where "n" is any positive whole number.
Golly, I hope that's right. I figured it out driving here today. Corrections welcome....
And, for those of you who were not already familiar with the Möbius Strip, make one out of newspaper and try splitting it into two rings with scissors, cutting all the way around on the center line. But first, to be fair, you should try to figure out what the result will be. If you can manage that without going crazy, try twisting the newspaper strip a full turn, rather than just a half-turn, before gluing the ends together. Even those of you who are familiar with the regular Möbius trick, will be hard-pressed to predict what happens when you split this one!
Of course, as my good friend Martin Gardner has commented to me, starting to cut one-third of the width from one edge of a regular half-twisted strip, leads to instant madness. But I should stop at this point, or else risk a considerable portion of the world's workforce closing down due to frustration....!
Thank you, sincerely, for your interest in
this page and in the puzzles we have presented. We hope that
you will be just as much interested in the work that we do here
at the JREF, and that you will see fit to support that work.
Next week, we'll take Leonardo off that turning wheel and show
you that there are two different - and correct - answers to that
problem.
